Problem Statement
In the diagram, two circles and a square lie between a pair of parallel lines that are a distance of 400 apart. The square has a side length of 279 and one of its sides lies along the lower line. The circles are tangent to each other, and each circle is tangent to one of the lines. Each circle also touches the square at only one point – the lower circle touches a side of the square and the upper circle touches a vertex of the square. If the upper circle has a radius of 65, then the radius of the lower circle is closest to
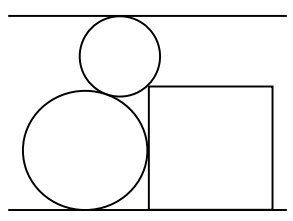
Solution
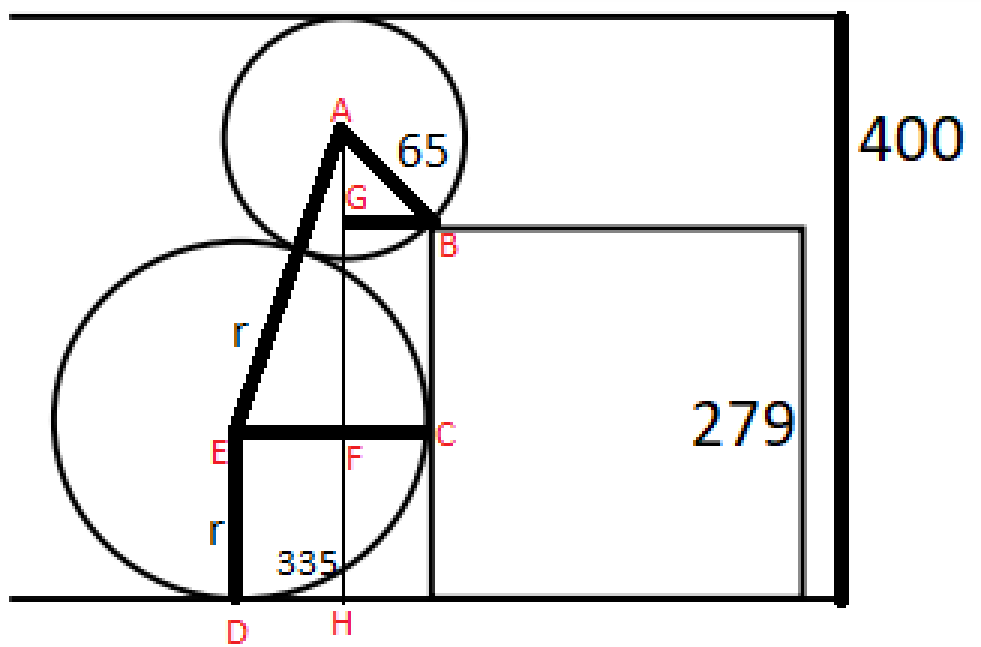$$\text {Since } \|AH\| = 400 - 65 = 335 \implies \|AG\| = \|AH\| - \|GH\| = 335 - 279 = 56$$ $$\text {From Pythagorean Theorem, } \|AB\|^2 = \|AG\|^2 + \|BG\|^2$$ $$65^2 = 56^2 + \|BG\|^2 \implies \|BG\| = 33$$ $$\text {Since } \|CE\| = \|EF\| + \|FC\| = r \implies \|CE\| - \|FC\| = \|EF\| \implies r - 33 = \|EF\|$$ $$\text {Since } \|AF\| + \|FH\| = 335 \implies \|AF\| + r = \|335\| \implies 335 - r = \|AF\|$$ $$\text {From Pythagorean Theorem, } \|AE\|^2 = \|AF\|^2 + \|EF\|^2$$ $$(65 + r)^2 = (335 - r)^2 + (r - 33)^2$$ $$65^2 + 130r + r^2 = 335^2 - 670r + r^2 + r^2 - 66r + 33^2$$ $$0 = r^2 - 866r + 109089$$ $$r = \dfrac{-(-866) \pm \sqrt{(-866)^2 - 4(1)(109089)}}{2(1)}$$ $$r = \dfrac{866 \pm 560}{2}$$ $$r = 153 \text { OR } r = 713$$ $$\text {Since } r < 400, \implies r = 153$$