Problem Statement
Square $PQRS$ has side length 4 m. Point $U$ is on $PR$ with $PR = 4UR$. A circle centered at $U$ touches two sides of the square. $PW$ is a tangent to the circle, with $W$ on $QR$. The length of $PW$, to the nearest thousandth of a metre, is
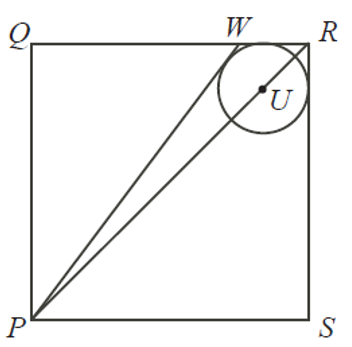
Solution
$$PR = \sqrt{PS^2 + PR^2} = \sqrt{32} = 4\sqrt{2}$$ $$\therefore UR = \sqrt{2}, UP = 3\sqrt{2}$$ $$\text{let } r \text{ be the radius of the circle.}$$ $$\therefore r^2 + r^2 = UR^2 = 2 \implies r = 1$$ $$\text{let } \theta \text{ be } \angle WPU \implies \angle QPW = 45 - \theta$$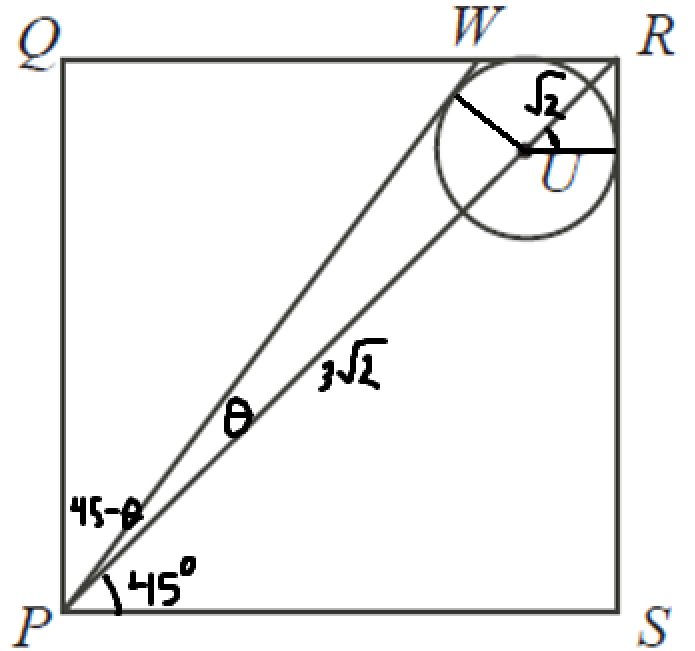
$$UP \sin(\theta) = UW \implies 3\sqrt{2} \sin(\theta) = 1$$ $$\therefore \theta = \sin^{-1}(\dfrac{1}{\dfrac{\sqrt{3}}{2}})$$ $$PW \cos(\theta) = PQ \implies PW = \dfrac{4}{\cos(\theta)}$$ $$\therefore PW \approx 4.685$$