Problem Statement
An ugly light fixture is hanging from point $O$ on the ceiling. Wires $OXM$, $OYN$ and $OZP$ pass through the vertices of a very thin wooden equilateral triangle $XYZ$ of side 60 cm. (A small bulb is attached to the end of each wire.) The plane of the wooden triangle is parallel to the ceiling. If each wire is 100 cm long and the lower end of each wire is 90 cm from the ceiling, what is the vertical distance between the wooden triangle and the ceiling?
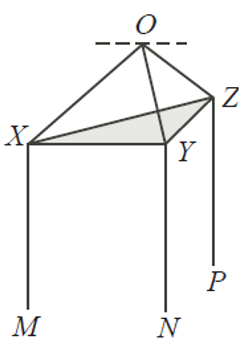
Solution
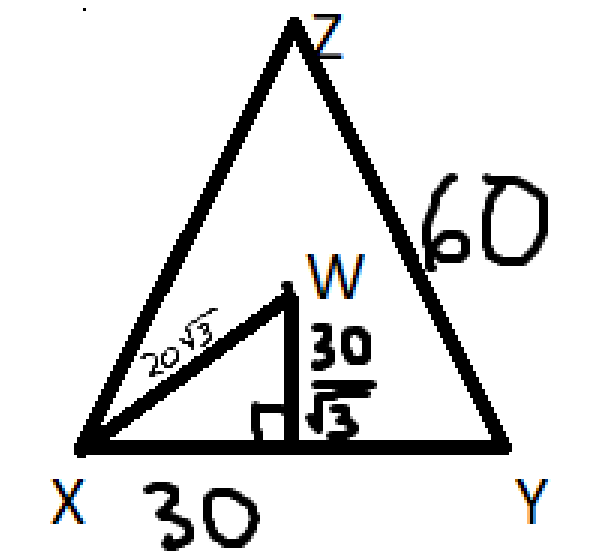$$\text{ let W be the centroid of } \triangle XYZ$$ $$OX^2 = WX^2 + OW^2$$ $$OX^2 = (20\sqrt{3})^2 + OW^2$$ $$OX + XM = 100$$ $$OW + XM = 90 \implies XM = 90 - OW$$ $$OX + 90 - OW = 100 \implies OX - 10 = OW$$ $$OX^2 = (20\sqrt{3})^2 + (OX - 10)^2$$ $$0 = 1200 - 20OX + 100 \implies OX = 65$$ $$OX^2 = (20\sqrt{3})^2 + OW^2$$ $$55 = OW$$