Problem Statement
In triangle $ABC$, if $AB = AC = x + 1$ and $BC = 2x - 2$, where $x > 1$, then the area of the triangle is always equal to
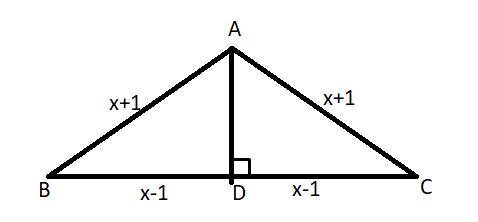
In triangle $ABC$, if $AB = AC = x + 1$ and $BC = 2x - 2$, where $x > 1$, then the area of the triangle is always equal to

A new version of content is available.