Problem Statement
In an art gallery, a 2 m high painting, $BT$, is mounted on a wall with its bottom edge 1 m above the floor. A spotlight is mounted at $S$, 3 m out from the wall and 4 m above the floor. The size of $\angle TSB$ is closest to
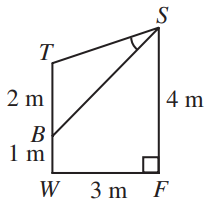
In an art gallery, a 2 m high painting, $BT$, is mounted on a wall with its bottom edge 1 m above the floor. A spotlight is mounted at $S$, 3 m out from the wall and 4 m above the floor. The size of $\angle TSB$ is closest to

A new version of content is available.