Problem Statement
In the diagram, $\triangle ABC$ is right-angled at $C$. If $BD = 2x$, $DC = x$, and $\angle ADC = 2(\angle ABC)$, then the length of $AB$ is
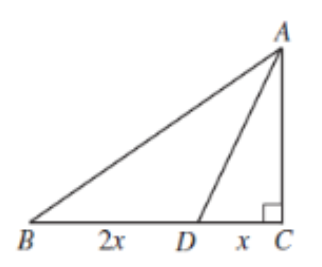
In the diagram, $\triangle ABC$ is right-angled at $C$. If $BD = 2x$, $DC = x$, and $\angle ADC = 2(\angle ABC)$, then the length of $AB$ is

A new version of content is available.