Problem Statement
In the diagram, $YQZC$ is a rectangle with $YC = 8$ and $CZ = 15$. Equilateral triangles $ABC$ and $PQR$, each with side length 9, are positioned as shown with R and B on sides $YQ$ and $CZ$, respectively. The length of $AP$ is
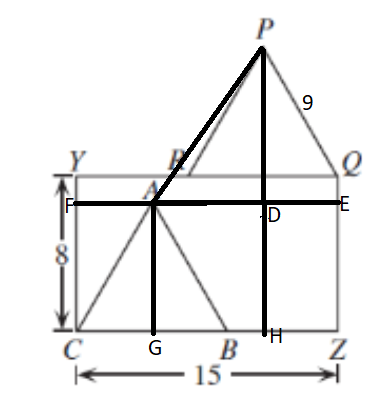
In the diagram, $YQZC$ is a rectangle with $YC = 8$ and $CZ = 15$. Equilateral triangles $ABC$ and $PQR$, each with side length 9, are positioned as shown with R and B on sides $YQ$ and $CZ$, respectively. The length of $AP$ is

A new version of content is available.