Problem Statement
A circle is tangent to three sides of a rectangle having side lengths 2 and 4 as shown. A diagonal of the rectangle intersects the circle at points $A$ and $B$. The length of $AB$ is
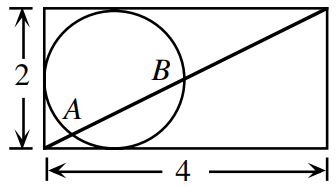
Solution
$$\text{ Let the radius of the circle be }r$$ $$\text{Since the circle is tangent to opposite sides of the rectangle, }\implies r = 1$$ $$\text{Let the origin } (0, 0) \text{ be the centre of the circle } \implies \text{ the equation of the circle }is x^2 + y^2 = 1^2$$ $$\text{Let } C(3, 1) \text{ and } D(-1, -1) \text{ be endpoints of the line segment}$$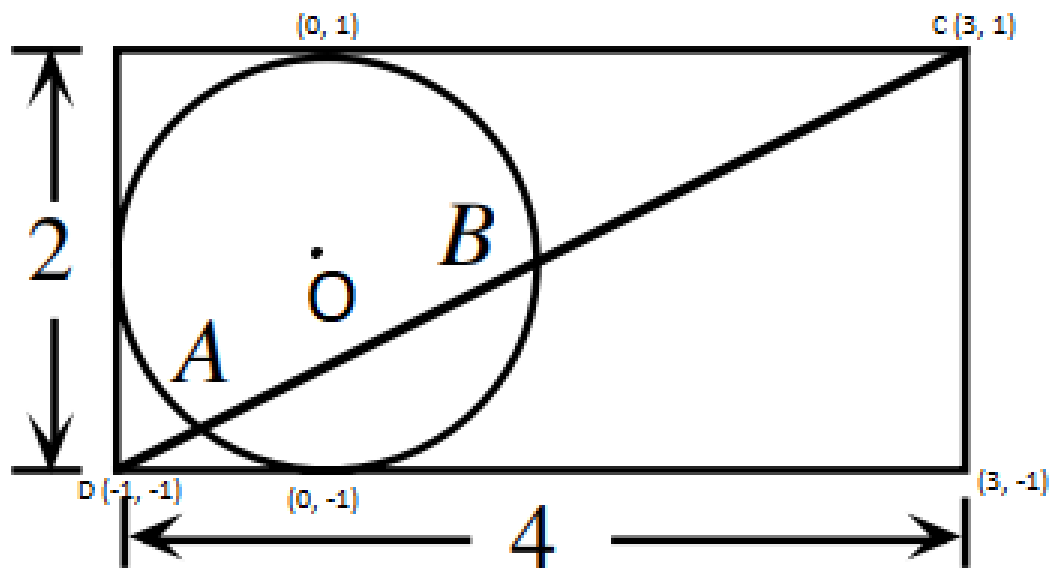
$$\text{Equation of the line CD: } y = mx + b$$ $$\text{Sub point } (3, 1)$$ $$(1) = \dfrac{-1 - 1}{-1 -3}(3) + b$$ $$\dfrac{-1}{2} = b$$ $$\therefore y = \dfrac{1}{2}x + \dfrac{-1}{2}$$ $$\text{Sub } y = \dfrac{1}{2}x + \dfrac{-1}{2} \text{ into } x^2 + y^2 = 1^2$$ $$x^2 + (\dfrac{1}{2}x + \dfrac{-1}{2})^2 = 1$$ $$x^2 + \dfrac{1}{4}x^2 + \dfrac{1}{4} - \dfrac{1}{2}x - 1 = 0$$ $$4x^2 + x^2 + 1 - 2x - 4 = 0$$ $$5x^2 - 2x - 3 = 0$$ $$(5x + 3)(x - 1) = 0$$ $$5x + 3 = 0 \implies x = \dfrac{-3}{5} \;\;\; \text{OR} \;\;\; x - 1 = 0 \implies x = 1$$ $$y = \dfrac{1}{2}(\dfrac{-3}{5}) + \dfrac{-1}{2} = \dfrac{-4}{5}$$ $$y = \dfrac{1}{2}(1) + \dfrac{-1}{2} = 0$$ $$\therefore A(\dfrac{-3}{5}, \dfrac{-4}{5}), \; B(1, 0)$$ $$AB = \sqrt{(\Delta x)^2 + (\Delta y)^2}$$ $$AB = \sqrt{(1 - \dfrac{-3}{5})^2 + (0 - \dfrac{-4}{5})^2}$$ $$AB = \sqrt{\dfrac{80}{5^2}} = \dfrac{4\sqrt{5}}{5}$$