Problem Statement
Two circles of radius 10 are tangent to each other. A tangent is drawn from the centre of one of the circles to the second circle. To the nearest integer, what is the area of the shaded region?
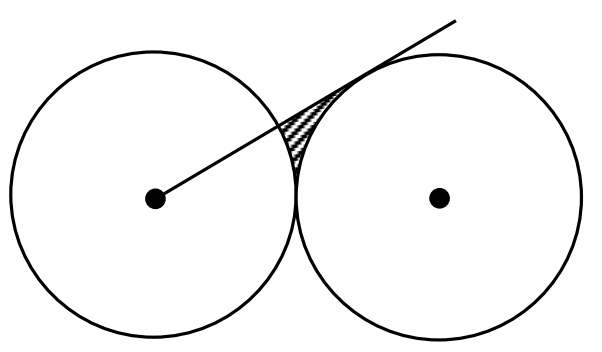
Solution
$$\text{Label the centres of the circles } A \text{ and } B$$ $$\text{Label the point where circle } B \text{ meets the tangent line point } C$$ $$\text{Since } AC \text{ is tangent to circle } B \implies \angle ACB = 90$$ $$AC^2 = AB^2 - BC^2$$ $$\therefore AC = 10 \sqrt{3}$$ $$\triangle ABC \text{ is a 30-60-90 triangle } \implies \angle A = 30^{\circ}, \angle B = 60^{\circ}, \angle C = 90^{\circ}$$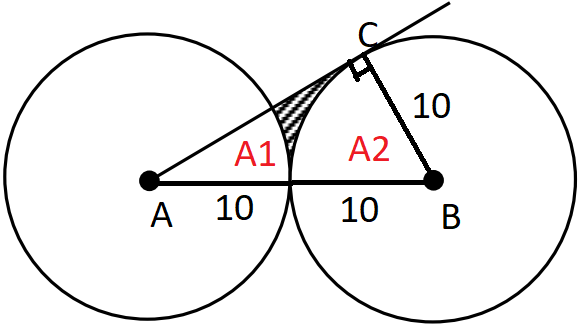
$$\text{Area of }\triangle ABC = A_1 + A_2 + A_S$$ $$\dfrac{1}{2} \times AC \times BC = (10^2 \times \dfrac{\angle A}{360} \times \pi) + (10^2 \times \dfrac{\angle B}{360} \times \pi) + A_S$$ $$\dfrac{1}{2} \times 10 \sqrt{3} \times 10 - (10^2 \times \dfrac{30}{360} \times \pi) - (10^2 \times \dfrac{60}{360} \times \pi) = A_S$$ $$A_S \approx 8$$