Problem Statement
Square $ABCD$ has sides of length 14. A circle is drawn through $A$ and $D$ so that it is tangent to $BC$, as shown. What is the radius of the circle?
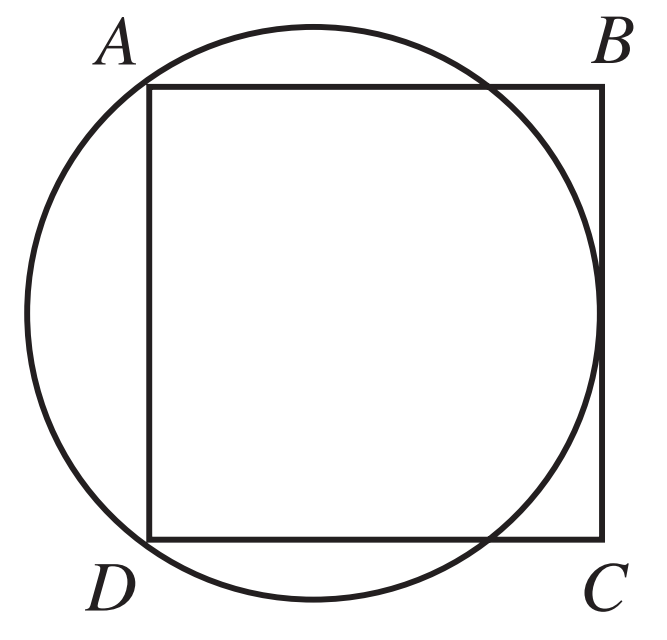
Solution
$$\text{Label the point the circle is tangent to } BC \text{ as point } E$$ $$\text{Label the point on the circle opposite to point } $E$ \text{ as point } $F$$ $$\text{Label the point where } EF \text{ intersects } AD \text{ as point } G$$ $$\text{Since} G \text{ bisects } AD \implies AG = GD = \dfrac{14}{2} = 7$$ $$\text{Let the radius of the circle be } r \text{ and } FG = x \implies GE = 2r - x$$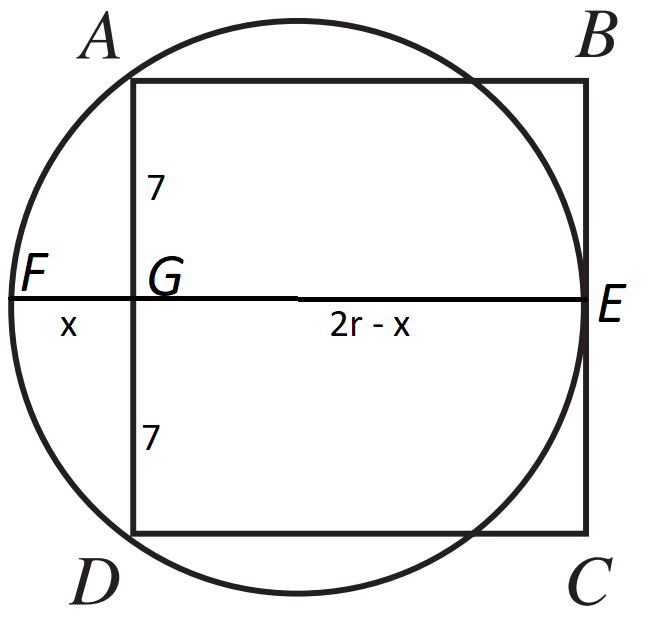
$$\text{By intersecting chord theorem, } FG \times GE = AG \times GD$$ $$x \times 14 = 7 \times 7$$ $$x = \dfrac{7}{2}$$ $$2r - x = 14$$ $$r = \dfrac{14 + \dfrac{7}{2}}{2}$$ $$r = \dfrac{35}{4}$$